689. Своппер
Перед
возвращением в штаб-квартиру Аазу и Скиву пришлось заполнить на местной таможне
декларацию о доходах за время визита. Получилась довольно внушительная
последовательность чисел. Обработка этой последовательности заняла весьма
долгое время.
– Своппер
кривой, – со знанием дела сказал таможенник.
– А что такое своппер? – спросил любопытный
Скив.
Ааз объяснил,
что своппер – это структура данных, которая умеет делать следующее:
·
взять отрезок чётной длины от x до y
и поменять местами число x с x + 1, x + 2 с x + 3, и т.д;
·
посчитать сумму на произвольном отрезке
от a до b.
Учитывая, что
обсчёт может затянуться надолго, корпорация “МИФ” попросила Вас решить проблему
со своппером и промоделировать ЭТО эффективно.
Вход. Состоит из одного или нескольких
тестов. В первой строке каждого теста записаны длина последовательности n и количество операций m (1 ≤ n, m ≤ 100 000).
Вторая строка теста содержит n целых
чисел, не превосходящих 106 по модулю – сама последовательность.
Далее следует m строк – запросы в
формате 1 xi yi – запрос первого типа, и 2
ai bi – запрос второго типа. Сумма всех n и m
по всему файлу не превосходит 200 000. Входные данные завершаются строкой из
двух нулей. Гарантируется, что xi
< yi, ai ≤ bi.
Выход. Для
каждого теста выведите ответы на запросы второго типа, как показано в примере.
Разделяйте ответы на тесты пустой строкой.
|
Пример входа |
Пример выхода |
|
5 5 1 2 3
4 5 1 2 5 2 2 4 1 1 4 2 1 3 2 4 4 0 0 |
Swapper
1: 10 9 2 |
РЕШЕНИЕ
структуры
данных – декартово дерево, неявный ключ
Анализ алгоритма
Заведем два
декартовых дерева с неявным ключом. Изначально занесем в первое числа, стоящие
на нечетных позициях (индексация начинается с 1), а во второе – числа на четных
позициях. Тогда операция своппера (запроса первого типа) будет заключаться в
вырезке двух участков деревьев и взаимной их переклейки.
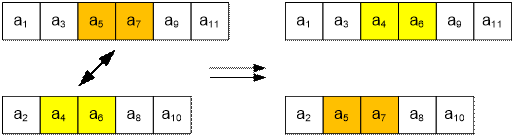
Например, пусть
изначально массив содержит 11 элементов. Поступает запрос первого типа с
параметрами x = 4, y = 7. Меняем местами части деревьев,
лежащие в интервале [4; 7] включительно. В данном случае следует поменять
местами (переклеить) интервалы (a5,
a7) и (a4, a6).
В каждой вершине
будем также поддерживать значение, равное сумме чисел в поддереве, для
котороого эта вершина является корнем. Это необходимо для эффективного
нахождения суммы чисел на отрезке.
Реализация алгоритма
Объявим
структуру Item вершины дерева с
неявным ключом. Элементы входной последовательности хранятся в значениях Value. В переменной Summa хранится сумма всех элементов последовательности в поддереве
с корнем в текущей вершине.
struct Item
{
int cnt,
Value, Priority;
long long Summa;
Item *l, *r;
Item() { }
Item (int
Value) : Priority((rand() << 16u) + unsigned(rand())),
Value(Value),
Summa(Value), l(NULL), r(NULL) { }
};
Объявим указатель Pitem на вершину дерева. Объявим два
декартовых дерева T1 и T2.
typedef Item* Pitem;
Pitem T1, T2;
Функция cnt возвращает количество
вершин в поддереве с корнем t.
int cnt(Pitem t)
{
return t ?
t->cnt : 0;
}
Функция GetSum возвращает сумму
элементов последовательности, хранящуюся в вершинах поддерева с корнем t.
long long
GetSum(Pitem t)
{
return t ?
t->Summa : 0;
}
Функция пересчета данных в вершине
t. Следует обновить количество вершин
t → cnt в поддереве t и сумму
t → Summa.
void upd(Pitem t)
{
if (t)
{
t->cnt = 1 + cnt(t->l) + cnt
(t->r);
t->Summa = t->Value + GetSum(t->l)
+ GetSum(t->r);
}
}
Слияние двух деревьев l и r
в t.
void Merge(Pitem l, Pitem r, Pitem
&t)
{
if (!l || !r)
t = l
? l : r;
else if (l->Priority > r->Priority)
Merge(l->r, r, l->r), t = l;
else
Merge(l, r->l, r->l), t = r;
upd(t);
}
Разбиваем дерево t по неявному ключу pos в l и r. В левое дерево заносится в точности pos вершин.
void Split(Pitem t, Pitem &l,
Pitem &r, int pos)
{
if (!t) return void( l = r =
0 );
if (pos <=
cnt(t->l))
Split(t->l, l, t->l, pos), r = t;
else
Split(t->r, t->r, r, pos - 1 -
cnt(t->l)), l = t;
upd(t);
}
Вычисляем суммы элементов
последовательности aL + …
+ aR. Ищем соответствующие
индексы суммируемых элементов в деревьях T1 и T2. Для T1
это будет интервал [L1, R1], а для T2
интервал [L2, R2]. Вырежем поддеревья с
ключами [L1, R1] и [L2, R2],
вычислим суммы элементов последовательности в них в переменной res, после чего склеим деревья обратно.
long long
Sum(int L, int
R)
{
if (L > R)
return 0;
int L1 = (L +
1) / 2, R1 = R / 2;
int L2 = L /
2, R2 = (R + 1) / 2 - 1;
Pitem A1, B1, C1, A2, B2, C2;
Split(T1,A1,B1,L1);
Split(B1,B1,C1,R1 - L1 + 1); // T1 = (A1, B1, C1)
Split(T2,A2,B2,L2);
Split(B2,B2,C2,R2 - L2 + 1); // T2 = (A2, B2, C2)
long long res = GetSum(B1) + GetSum(B2);
Merge(A1,B1,B1); Merge(B1,C1,T1);
Merge(A2,B2,B2); Merge(B2,C2,T2);
return res;
}
Реализация операции своппера на
отрезке [L; R] четной длины. Вырезаем соответствующие интервалы [L1, R1] и [L2,
R2] из деревьев T1
и T2 и меняем их местами.
void Swap(int
L, int R)
{
int L1 = (L +
1) / 2, R1 = R / 2;
int L2 = L /
2, R2 = (R + 1) / 2 - 1;
Pitem A1, B1, C1, A2, B2, C2;
Split(T1,A1,B1,L1);
Split(B1,B1,C1,R1 - L1 + 1); // T1 = (A1, B1, C1)
Split(T2,A2,B2,L2);
Split(B2,B2,C2,R2 - L2 + 1); // T2 = (A2, B2, C2)
Merge(A1,B2,B2);
Merge(B2,C1,T1); //
T1 = (A1, B2, C1)
Merge(A2,B1,B1);
Merge(B1,C2,T2); //
T2 = (A2, B1, C2)
}
Основная часть программы. Читаем
входные данные. Строим декартовы деревья T1 и T2.
while(scanf("%d
%d",&n,&m) , n + m)
{
T1 = T2 = NULL;
if (cs != 1)
printf("\n");
printf("Swapper
%d:\n",cs++);
for(i = 1; i
<= n; i++)
{
scanf("%d",&val);
if(i&1)
Merge(T1, new Item(val), T1);
else
Merge(T2, new Item(val), T2);
}
Последовательно обрабатываем
запросы.
for(i = 0; i
< m; i++)
{
scanf("%d
%d %d",&type,&a,&b);
a--; b--;
if (type ==
1)
Swap(a,b);
else
printf("%lld\n",Sum(a,b));
}
}